In Defense of Vanilla DPO for Language Model Alignment
Direct Preference Optimization (DPO; Rafailov et al., 2023) has emerged as the de-facto alignment algorithm for language models. It has been employed by many industrial level language models, which includes but is not limited to Meta’s Llama 3 (Dubey et al., 2024), AI2’s Tulu (Lambert et al., 2024), Alibaba’s Qwen (Yang et al., 2024). The intuition is that DPO aims to directly increase the log-likelihood of human-preferred responses while decreasing the log-likelihood of dispreferred ones. Compared to standard RLHF (Stiennon et al., 2020), the asymptotically equivalent DPO shines due to its simplicity - It requires neither on-policy sampling nor training a separate reward model.
Despite its simplicity and effectiveness, DPO has faced many criticisms (Chen et al., 2024, Pal et al., 2024,Rafailov et al., 2024,Razin et al., 2024, Meng et al., 2024, Cho 2024). We summarize the criticisms below:
-
Likelihood Displacement: The likelihood of the chosen and the rejected response simultaneously decreases. Existing work accounts this to either the edit distance between the chosen and the rejected is short (Pal et al., 2024) or the embedding distance the chosen and rejected is small (Razin et al., 2024). Too similar pairs make the model fail to differentiate between the chosen and the rejected, resulting in the model simutaneously reducing the likelihood of both.
-
Poor Ranking Accuracy: Even after DPO, the model fails to assign higher probability to chosen responses compared to rejected responses (Chen et al., 2024). This is an expected outcome due to likelihood displacement.
-
Mismatch Between Data and Policy: During pure offline DPO, where the preference data are collected from various models, e.g., Ultrafeedback (Cui et al., 2024), there exists a mismatch between what the model can generate and what is optimized. To mitigate this issue, there has been many works that propose on-policy DPO (Xu et al., 2024, Guo et al., 2024, Yuan et al., 2024) that generates the pair of responses from the reference policy rather than collecting preferences offline. Another solution would be to train the model first on chosen responses (Meng et al., 2024).
A natural question arises: despite all these criticisms, why is vanilla DPO still the go-to algorithm when aligning language models?
In this blogpost, I aim to give a non-rigorous explanation of the following two research questions:
- Why does the likelihood displacement phenomenon occur?
- Why DPO works despite likelihood displacement on off-policy data?
By answering these questions, I aim to defend against vanilla DPO for alignment, and to shed light on a deeper understanding of what DPO is doing to our model.
Preliminaries:
For a given user prompt \(x\), the language model \(\pi(\cdot \mid x)\) yields a probablity distribution over all possible responses \(\mathbf{y}\).
The pipeline begins with training the base language model \(\pi_\text{base}\) on high-quality generations \(\mathcal{D}_\text{SFT} = \{(x, \mathbf{y}), ...\}\). The SFT loss is given by
\[\mathcal{L}_\textrm{SFT} = - \log \pi(\mathbf{y} \mid x)\]This stage of the pipeline is called Supervised Fine-Tuning (SFT), which produces the SFT’ed model \(\pi_\textrm{SFT}\).
Then there is another dataset \(\mathcal{D}_\textrm{DPO} = \{(x, \mathbf{y}_w, \mathbf{y}_l) ... \}\), where there are two generations \((y_w, y_l)\) for a given prompt \(x\), where \(\mathbf{y}_w\) is preferred (usually referred to as the “winning” or “chosen” response), and \(\mathbf{y}_l\) is dispreferred (usually referred to as the “losing” or “rejected” response). The DPO loss is given by:
\[\mathcal{L}_\textrm{DPO} = -\log \sigma\left(\beta\log \frac{\pi_\theta(\mathbf{y}_w \mid x)}{\pi_\text{SFT}(\mathbf{y}_w \mid x)} - \beta\log\frac{\pi_{\theta}(\mathbf{y}_l \mid x)}{\pi_\textrm{SFT}(\mathbf{y}_l \mid x)}\right),\]which aims to maximize the margin between the increase in log-probability of the chosen response \(\log \pi_\theta(\mathbf{y}_w \mid x) - \log \pi_\text{SFT}(\mathbf{y}_w \mid x)\), and the increase in log-probability of the rejected response \(\log \pi_\theta(\mathbf{y}_l \mid x) - \log \pi_\text{SFT}(\mathbf{y}_l \mid x)\). In an ideal setting, the DPO loss should push the log-likelihood of the chosen response higher and push the log-likelihood of the rejected response lower, making the preferred response more likely under the aligned model.
However, as many works have noticed (Rafailov et al., 2024, Pal et al., 2024, Razin et al., 2024, Feng et al., 2024), often times the likelihood of both the chosen and the rejected response goes down, a phenomenon that Razin et al., 2024 terms “likelihood displacement”. In this blogpost, I would like to offer another explanation of why does “likelihood displacement” happens and more interestingly, why DPO is a strong baselines despite “likelihood displacement”. To this, we first need to investigate the effect of DPO onto the language modeling distribution — “The Squeezing Effect”.
The Squeezing Effect of DPO Negative Gradient
The DPO gradient consists of two parts, a positive gradient that increases the likelihood of the chosen response, and a negative gradient that decreases the likelihood of the rejected response. Feng et al., 2024 shows that the negative gradient trumps the positive one.
If we take one step further and dig into the negative gradient, Ren and Sutherland, 2024 introduced an interesting effect of the negative gradient in DPO: both the chosen and rejected response goes down, and as a result, the majority of the probability mass is carried to sequences with very high likelihood. Intuitively, the “rich gets richer”, i.e. sentences with already high probability gets even higher due to the DPO negative gradient.
In the paper, they wrote as:
”The decreased probability mass is largely “squeezed” into the output which was most confident before the update. That is, if \(y^* = \arg \max_{i \in [V]\backslash \{y_l\}} \pi_{\theta}^t(y = i)\) , then \(\pi_{y = y^*}\) is guaranteed to increase.“
The following figure from Ren and Sutherland, 2024 illustrates the squeezing effect of DPO. As the log-likelihood of the rejected sentence \(\pi(\mathbf{y}_{u}^-)\) gets pushed down, the majority of the increased mass goes to \(\mathbf{y^*}\), the most probable sentence, instead of the chosen (winning) sentence \(\mathbf{y}_u^{+}\).
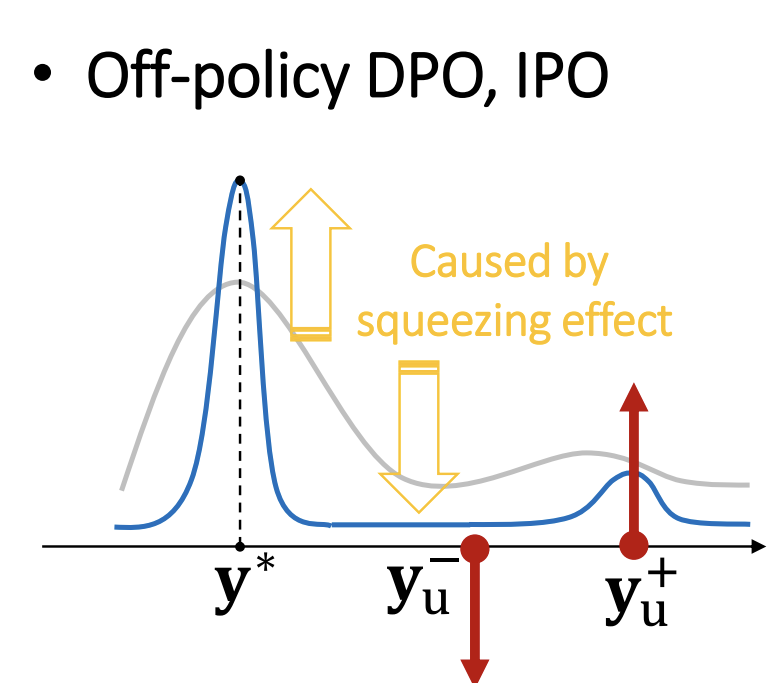
To validate this claim, Ren and Sutherland, 2024 performed a series of experiments: they plot out the log-likelihood of the chosen sentence and its paraphrases, the rejected sentence and its paraphrases, and a proxy of \(\mathbf{y}^*\) - the greedy decoded sentence: the following figure from the paper illustrates this:

In the left 4 subfigures, we observe that the likelihood of the chosen and its paraphrases, the rejected and its paraphrases all get decreased during DPO. However, the greedy decoded sentence, which is the black one in the rightmost subfigure goes up, thus confirming that the most the the probability mass goes to \(\mathbf{y}^*\)(or at least a proxy of \(\mathbf{y}^*\)).
Therefore, we can give a explanation of why “likelihood displacement” happens: it is due to the DPO negative gradient squeezes the probability masses to \(\mathbf{y}^*\) , often leading to decrease of both \(\pi(\mathbf{y}_w \mid x)\) and \(\pi(\mathbf{y}_l \mid x)\). Now we aim to answer the second question: why are the benefits of increasing \(\mathbf{y}^*\)?
The Benefits of Increasing \(\mathbf{y}^*\)
Now that we know the reason why DPO decreases both the chosen and the rejected response is because it carried most of the decreased probability mass to \(\mathbf{y}^*\), we want to know why DPO, even the naive offline version, is still able to yield strong baselines, and is often the go-to method for industry labs to build strong models.
It turns out that \(\mathbf{y}^* = \arg\max_\mathbf{y} \pi(\mathbf{y} \mid x)\) itself is a very strong baseline. In Huang et al., 2024, the authors were interested in the mechanisms behind self-improvement - why can language models be improved when training on data that is generated by itself (Yarowsky, 1995, He et al., 2020, Zelikman et al., 2022, Xu et al., 2023), sometimes even without external feedback (Yuan et al., 2024)?
Huang et al., 2024 points out that the best-of-N response with the highest likelihood: \(\mathbf{\hat{y}}^* = \arg\max_{\mathbf{y}_i,~i \in \{1,...,N\}} \pi(y_i\mid x)\) is actually a strong baseline, and training a language model on high-likelihood responses can “sharpen” the model towards these high-likelihood responses. (It would be interesting to track the best-of-N log-likelihood throughout DPO).
Empirically, Huang et al., 2024 validated their results on a large suite of models (Phi, Mistral, Llama, GPT-3.5) across various tasks (MATH, GSM, …). The results are in the following figure:
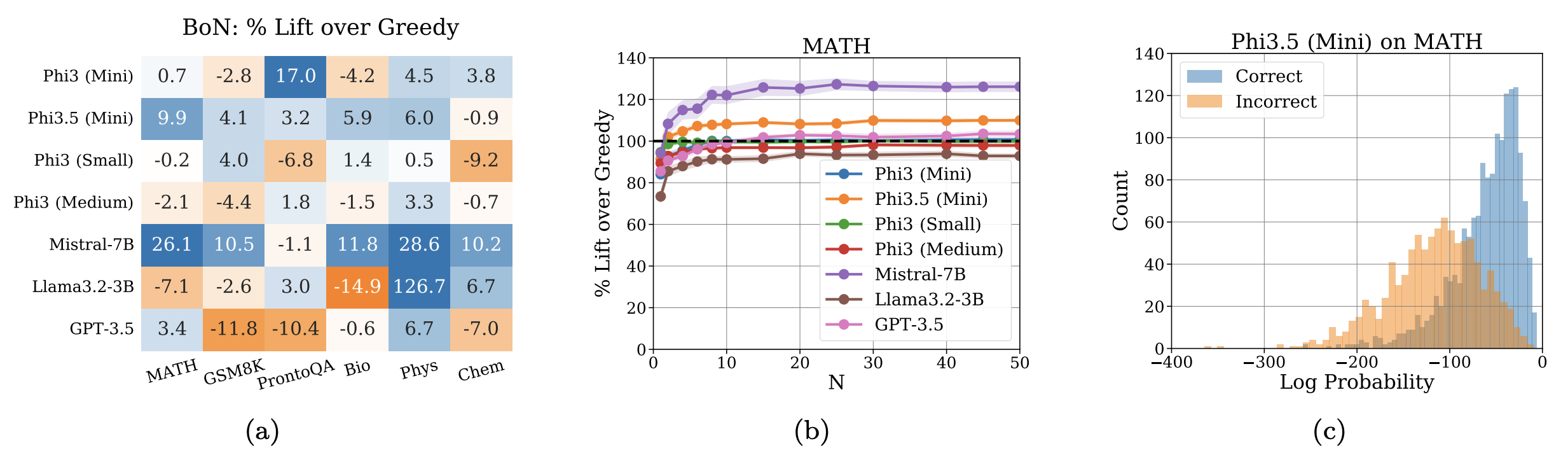
In subfigure (a), the numbers refer to the percent accuracy improvement over greedy decoding. The authors find that:
- Best-of-N (with highest log-likelihood) is always better than naive sampling with temperature = 1.0
- For all datasets, Best-of-N improves upon greedy decoding, for at least one model.
- For every model, there is at least one dataset where Best-of-N improves upon greedy decoding.
In the middle subfigure (b), x-axis is the N in best-of-N and the y-axis is the percentage improvement over greedy decoding - this shows that finding sequences with high likelihood is able to yield a much stronger baseline than greedy decoding (which is already a strong baseline).
In the right subfigure (c), the histograms of correct and incorrect responses are plotted, we can see that the correct response tends to have higher likelihood under the base model.
These findings indicate that the “hidden knowledge” for self-improvement is hidden at the probabilities - sequences with high log-probability is more likely to be correct. \(\mathbf{y}^*\) , or the most probable sentence is most likely to be correct.
So far, we have learned that:
-
DPO pushes up sentences with super high log-probability under the model, especially when the winning and losing response are offline samples (Ren and Sutherland, 2024).
-
Sentences with super high log-probability are more likely to be correct answers / better responses (Huang et al., 2024).
Now, It should be intuitive that why DPO (even the offline variant) is able to yield a strong baseline - it “squeezes” or “sharpens” up the log-likelihood of sentences with already large log-probability, regardless of the winning and losing response construction (because it is very unlikely that the winning and / or the losing response is \(\mathbf{y}^*\)). There is also empirical evidence that performing vanilla DPO on “wrong-over-wrong” responses (Yao et al., 2024) can improve performance.
Limitations
Admittedly, this explanation of DPO moves masses to \(\mathbf{y}^*\) is a simplified version of what is happening in practice, otherwise we would be living in a world where we simple impose the negative gradient on every offline data to sharpen the model towards high log-prob sentences. But I think this explanation is interesting and motivates to think of more reliable reward signals beyond model log-probs.