Manipulating Gradients to Balance Multilingual Machine Translation Models
Overview
Finding out the reasons and solutions for negative interference in Multilingual Neural Machine Translation [Johnson et al., 2016; Aharoni et al., 2019] has been an active research area for the past 5-7 years. Yet, while previous studies [Wang et al., 2020] find that negative interference mainly occurs between different language families, recent studies [Shaham et al., 2023] have demonstrated that negative inference does not happen between languages of different families. The interference emerges because of the mismatch in the amount of data for different translation directions. Real-world translation data suffers from a heavy mismatch of data in different directions, ranging from less than 100K to over 100M [NLLB Team, 2022], so it is crucial to find balancing methods that are both scalable and robust.
This blog post aims to give an overview of the two approaches for handling imbalances in multilingual neural machine translation: Scalarization and Gradient projection. Both methods have pros and cons, and there still needs to be a consensus on which method performs the best. This blog post will cover some of the most up-to-date methods for handling data size mismatches and interference.
Disclaimer: The papers introduced in this blog post are only representative works rather than a comprehensive survey to give an overview of the different methods to handle data imbalance in translation directions.
Background
Multilingual Neural Machine Translation
We start by describing some basics in multilingual neural machine translation: we are interested in mapping a source sequence \(\textbf{x}_s = \{x_1, x_2, ..., x_n\}\) in language \(s\) to a target sequence \(\textbf{y}_t = \{y_1, y_2, ..., y_m\}\) in language \(t\). We train an autoregressive model parameterized by \(\theta\) that predicts each target token conditioning on the entire source sentence and the target tokens before it:
\[\mathcal{L}_{s,t}(\theta) = \sum_{i=1}^m \log p_\theta(y_i \mid \mathbf{y}_{<i}, \mathbf{x}).\]In multilingual neural machine translation, multiple source-target pairs are concatenated to form a large dataset. Given parallel sentences in \(N\) languages pairs \((s_1, t_1), (s_2, t_2),... (s_N, t_N)\), a naive multilingual machine translation model aims to minimize an unweighted sum of the losses of individual translation directions:
\[\mathcal{L}_\text{MMT}(\theta) = \sum_{i=1}^N \mathcal{L}_{s_i, t_i}(\theta)\]Here, the parameters for each translation direction are shared, which is much more compute-efficient than training individual models for each direction. Different directions might benefit from each other, resulting in positive transfer.
Pareto Front
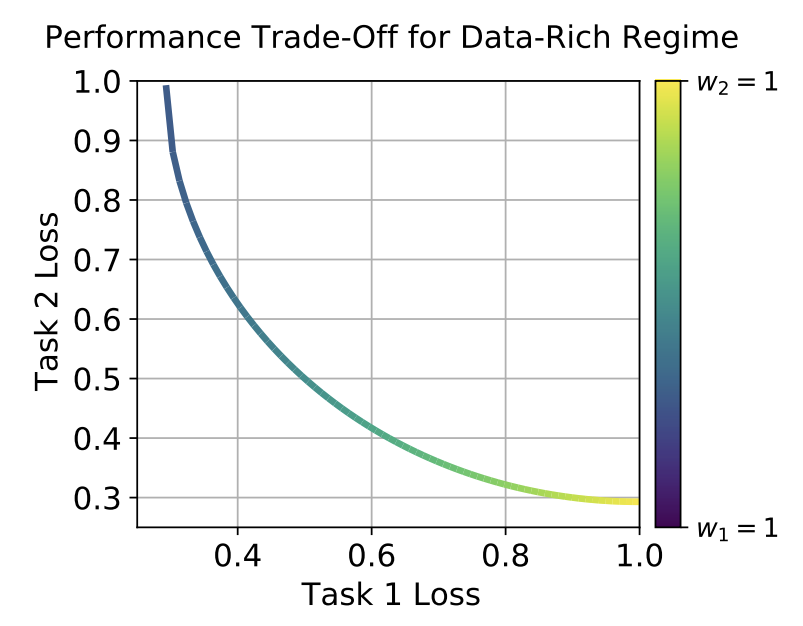
Multilingual Translation can be seen as a multi-task learning (or multi-objective optimization) problem [Ahroni et al., 2019], where each translation direction is an individual task. We are interested in finding the optimal solutions in that we cannot improve the performance of an individual task without sacrificing the performance of other tasks. Such solutions are called Pareto optimal solutions [Boyd and Vandenberghe, 2004]. The set of all Pareto optimal solutions forms the Pareto Front of a given multi-objective optimization problem. See Figure 1 for an illustration of the Pareto front (figure pasted from Fernandes et al., 2023).
Scalarization
The heavy mismatch in data sizes causes the naive unweighted average of individual losses to amplify the performance of high-resource languages (HRLs) and decrease the performance of low-resource languages (LRLs). In practice, we sample a batch of input and output sentences. Since data of HRLs can be more than 10x of data of LRLs, we are far more likely to sample from HRLs, resulting in the optimization process heavily favoring optimizing towards better performance on HRLs.
To mitigate this, instead of using proportional sampling, we can use temperature sampling [Arivazhagan et al., 2019]. The probability of sampling from each direction is given by:
\[p_{(s_i, t_i)} = \frac{D(s_i, t_i)^\frac{1}{\tau}}{\sum_{j=1}^N D(s_j, t_j)^\frac{1}{\tau}}\]Where \(D(s_i, t_i)\) is the datasize of translation direction \(s_i \rightarrow t_i\) , and \(\tau\) is the sampling temperature. When \(\tau = 1\), our sampling method is equivalent to naive proportional sampling. As \(\tau\) gets larger, we are decreasing the weights on HRLs and increasing the weights on LRLs. As \(\tau \rightarrow +\infty\), the sampling strategy becomes a uniform distribution over all language pairs.
A common understanding in the machine translation literature is that tuning the temperature \(\tau\) is equivalent to tuning the weights for each translation direction in a weighted sum of individual losses, which we refer to as scalarization.
\[\mathcal{L}_\text{MMT}(\theta) = \sum_{i=1}^N w_i \mathcal{L}_{s_i, t_i}(\theta)\]Although the equivalency of tuning the temperature \(\tau\) and tuning the weights \(w_i\) have not been thoroughly established, in this blog post, I will use sampling ratio and task weights interchangeably and introduce some of the latest advances in how to find fantastic weights that achieves good performance.
Static Weights
Fernandes et al., 2023 show we can find the Pareto front for multilingual translation by varying the sampling ratio. However, their work assumes that we have an even amount of data for each translation direction, which is often untrue in real-world settings. A follow-up work [Chen et al., 2023] shows that when there is a data size mismatch, the Pareto front collapses: see the following figure from the paper for a comparison between the Pareto curve when data is balanced VS data is imbalanced.

Chen et al., 2023 presents a comprehensive study on how to tune the sampling temperature (or, equivalently, task weights) for each translation direction. Given a fixed sampling ratio \(p\) and the number of training examples \(D\) for a given direction, the cross-entropy loss can be expressed as:
\[\mathcal{L}(p, D) = (k\cdot p)^{-\alpha} + (D^\gamma + b) \cdot(q\cdot p)^{\beta}+M_{\infty}\]The given parameters are the sampling ratio \(p\), the data size \(D\), and a constant bias term \(M_{\infty}\), and the rest of the parameters are to be estimated. To estimate these parameters, the authors conducted a series of experiments on WMT \(\text{English} \rightarrow \{\text{French, German}\}\) data and varied the amount of available data \(D\) and sampling ratio \(p\) to form a curve and estimate parameters that best fit this curve. Experiments show that their estimated scaling laws also generalize to other language pairs.
So the question remains: how to find the best \(p\) for each direction? The author frames this as an optimization problem: given a fixed number of \(D\) and a pre-defined importance of each translation direction \(r\) for each task, the optimization problem is:
\[\mathbf{p} = \arg\min_p \mathcal{L}(p;r;d)\] \[\textrm{subject to}~\mathcal{L(\mathbf{p};r;d}) = \sum_{i}r_i\mathcal{L}(p_i, D_i)\] \[\mathbf{p}>0\] \[\sum_{i} p_i =1,~~~\sum_{i} r_i =1\]The standard way is to assume each translation direction has equal importance \(r_i = \frac{1}{N}\), but this is customizable if you want to emphasize some translation directions. Such a static weighting method for multilingual translation produces strong baselines over using a fixed temperature (e.g., \(\tau = 1, 5, 100\)) and fancy gradient projection techniques (which we will introduce later).
Dynamic Weights
But why do we need static weights for each direction? The mismatch in data sizes causes a mismatch in convergence rates, as Huang et al., 2022 points out, while LRLs have already converged, the HRLs have not yet converged, and continuing training on all tasks results in overfitting on the LRLs. This motivates methods that tackle the imbalanced problem with dynamic sampling temperature methods that consider that different directions converge at different rates.
A naive way is to focus on one or a set of translation directions that converges the slowest during training: In statistical learning, Distributionally Robust Optimization methods [Oren et al., 2019; Sagawa et al., 2020; Zhou et al., 2021], instead of minimizing the sum of all losses, tries to minimize the loss of the worst performing group, forming a min-max optimization problem:
\[\min_\theta \max_{s, t} \mathcal{L_{s ,t}(\theta)}\]However, naively minimizing the worse-performing language pair ignores the fact that several translation directions might have similar data sizes and thus have similar bad performance, so instead of only focusing on the one worse-performing direction, both Oren et al., 2019 and Zhou et al., 2021 proposes to minimize the loss of a set of worse performing domains/languages.
Specifically, Oren et al., 2019 minimize a fixed fraction of worse performing domains in general language modeling.
Zhou et al., 2021 minimizes the worst-case weight average loss of all language pairs, where the weights/sampling ratios are close to proportional sampling. More intuitively, the author first finds some adversarial weights that are close to proportional weights but yields the worst possible loss of all the weights that are close and aims to minimize this loss. Again, you can be creative in how to define closeness for two probability distributions, but in their work, they used the \(\chi\)-Divergence because it has some nice properties [Duchi and Namkoong, 2016; Hashimoto et al., 2018].
Experiment results show that maximizing the worst-case loss can improve the performance of LRLs while minimally sacrificing the performance of HRLs, essentially pushing forward the Pareto frontier.
Li and Gong, 2021 find weights for each direction that guide the optimization process towards a flatter minimum. The improvements are more significant compared to our previously introduced Distributionally Robust Optimization works, which highlight that the optimization process for multilingual translation should take the differences in convergence (or, in this case, curvature) into account.
We can also make the weights learnable. Depending on how to measure how well is the training process going, we bias our sampling ratio towards training regimes that are well.
For example, we can select a sampling ratio so that our training gradient is most similar to the development gradient [Wang et al., 2020].
We can also select a sampling ratio to minimize loss-related definitions of learning progress. [Kreutzer et al., 2021].
But, perhaps the simplest of all methods is more robust and generalizable:
Instead of searching for these fantastic weights, why don’t we train on HRLs and then train on a mixture of HRLs and LRLs? Well, it turns out this simple method works surprisingly well:
Choi et al., 2023 proposes to first train on HRLs, then “fine-tune” on a mixture of HRLs and LRLs, which is equivalent to tuning the temperature but in a more coarse-grained way. Instead of using the training signals (gradient, activations), this work manually divides the training into two stages - training on HRLs first and a mix of high and low resource languages second. This simple trick solves the mismatch in convergence that causes overfitting on the LRLs.
Gradient Projection
It was not until recently [Xin et al., 2022] that we realized we don’t need fancy techniques designed for multi-task learning to solve unbalanced training in multilingual translation. Simple scalarization often yields strong baselines that are tough to beat. However, there have been extensive studies on how to manipulate the gradients in general multi-task learning setups, and people have been trying them on multilingual machine translation.
It is natural to assume that the gradient conflict between different tasks causes interference. Therefore, prior research has developed methods to either drop some of the conflicting gradients [Chen et al., 2020], project one gradient to the orthogonal plane of another [Yu et al., 2020; Yang et al., 2021], or taking language similarity into account and project one gradient to a plane where the cosine similarity between gradients reflect language similarity [Wang et al., 2020]. See the following figure for an illustration of these methods:
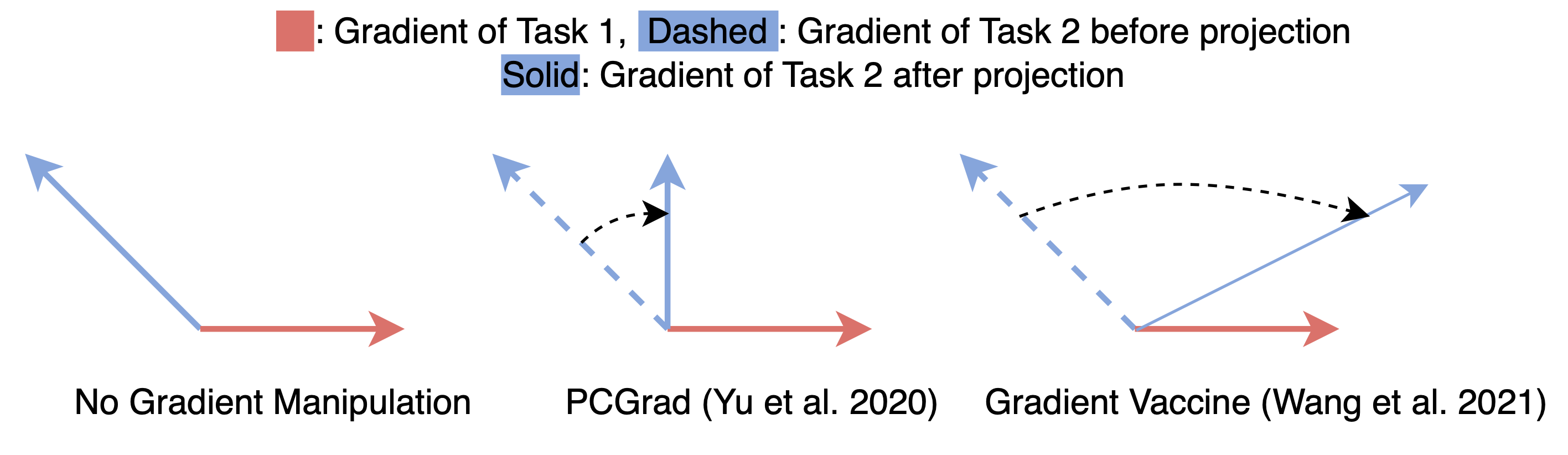
Not surprizingly, Wang et al., 2020 finds that the gradient similarity positively correlates with language familiies, i.e. languages from the same family are likely to have similar gradients. I reproduced some of their results in a English-to-many multilingual translation setting and found that the gradient similarity seems to have more to do with language order than script:
| Similar script, Same order | Gradient Similarity |
|---|---|
| French, Portugese | 0.35 |
| Different script, same order | |
| French, Russian | 0.13 |
| French, Korean | 0.22 |
| Similar script, different order | |
| Chinese, Japanese | 0.06 |
| French, Turkish | 0.12 |
| Different script, different order | |
| French, Japanese | 0.06 |
| Chinese, Korean | 0.008 |
As promising as gradient projection methods might seem, there has been compelling evidence recently that gradient deconfliction does not outperform simple static scalarization in the general multi-task learning setting [Xin et al., 2022; Kurin et al., 2022] and specifically for machine translation [Chen et al., 2023].
Discussion and Future Work
As you can see, a lot of the papers introduced here are from the past one or two years, so the whole area of how to elegantly handle the data size mismatch in multilingual translation is still a trendy topic.
We also see that scalarization and gradient projection modify two different parts of the gradient: scalarization mostly operates on the magnitude, and projection mainly operates on the direction (but magnitude is also involved).
Future Directions
Here are some of my thoughts on future directions here: all are challenging but exciting to pursue, and I envision myself working in these directions.
-
Find better ways to do dynamic scalarization without additional computational overhead - also needs to have strong improvements over Choi et al., 2023.
-
Understand the optimization landscape of multilingual translation - and find which findings generalize to other deep multi-task settings (e.g., instruction tuning, LM pre-training) and also strong generalizability (e.g., zero-shot translation). One prevailing understanding is that many-to-one multilingual MT behaves more like general multi-task learning while yielding large improvements in the one-to-many setting is hard.
-
Scale up! Language Model pre-training needs to find weights for each domain. Anil et al., 2022 did a grid search on the weights, which is expensive. There are many open questions: should these weights be static or dynamic? what is the most important factor when finding these weights [Xie et al., 2023a, Xie et al., 2023b] - as simple as size? what about quality? How do we find scalable methods to measure pre-training data quality/diversity?